在试卷现实生活中, 总是会碰到一些泛函上的最优化问题. 它们大多可以归为以下形式:
在函数集合
$$ \left\{ x(t) \ \Big| \ x(t_1) = y_1, x(t_2) = y_2, x^{(k)} 存在 \right\} $$
中, 求一个函数 $x(t)$ 使得泛函 $I[x(\centerdot)]$ 的积分:
$$ S = \int_{t_1}^{t_2} I[x, x’, t] \ \mathrm{d}x $$
有极值.
我们知道, 一个连续函数 $x(t)$ 的在某个值 $t$ 有极值的必要条件是 $x’(t) = 0$, 这被称为费马引理 (强烈建议先去看看它的证明, 其证明的思想有助于理解下文).
那么对于泛函, 这个必要条件是什么呢?
在微积分中, 我们的一般思考方法是取极值附近的一个微元 $\mathrm{d}x$, 然后利用函数的连续性去取得极值的必要条件, 在泛函中我们能否也去考虑一个极值函数附近的某种"微元", 即对于对应极值函数的一个小小的偏移函数, 借此来研究极值函数符合的条件呢?
我们来(随便)构造一个函数 $\mathrm{\eta}(t)$, 令其连续且存在 $k$ 次导数, 并且还要在两端点为 $0$, 不妨令:
$$ \eta(t) = (t - t_1)^{2k} (t - t_2)^{2k} $$
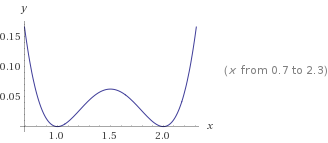
$$let\ (k=1, t_1=1, t_2=2)$$
显然它符合我们的要求, 并且图像看起来就像肿了一个小包, 也挺符合我们对"偏移函数"的认知(大概?)
有了偏移函数还不够, 我们在泛函中没办法搞到像在实数集一样的序性质, 也就没办法用费马引理的老路子, 那咋办啊?
既然我们都已经有偏移函数了, 不妨引入一个实数 $\alpha$, 它能控制"偏移的量", 这就把泛函的偏移归结为实数的偏移,然后我们就能用费马引理愉快(?)地玩耍了.
我们先随便找一个函数 $x_0$, 并令它偏移一下变成 $x = x_0 + \alpha \eta$, 然后我们的 $S$ 就从一个关于 $x$ 的泛函变成了一个关于 $\alpha$ 的函数:
$$ S(\alpha) = \int_{t_1}^{t_2} I[x_0 + \alpha \mathrm{\eta}, x_0’ + \alpha \mathrm{\eta}, t]\ \mathrm{d}t $$
当这个函数 $S(\alpha)$ 有极值时我们必有: $\mathrm{d}S/\mathrm{d}\alpha = 0$. 我们对 $\alpha$ 求导, 有:
$$ \frac{\mathrm{d}S}{\mathrm{d}\alpha} = \int_{t_1}^{t_2} \frac{\mathrm{d}}{\mathrm{d}\alpha} I[x_0 + \alpha \mathrm{\eta}, x_0’ + \alpha \mathrm{\eta}, t] \ \mathrm{d}t $$
利用多元函数的全微分, 有:
$$ \frac{\mathrm{d}I}{\mathrm{d}\alpha} = \frac{\partial I}{\partial x} \frac{\mathrm{d}x}{\mathrm{d}\alpha} + \frac{\partial I}{\partial x’} \frac{\mathrm{d}x’}{\mathrm{d}\alpha} + \frac{\partial I}{\partial t} \frac{\mathrm{d}t}{\mathrm{d}\alpha} $$
注意到最后一项中 $t$ 并不依赖于 $\alpha$, 所以原式化为:
$$ \frac{\mathrm{d} S}{\mathrm{d} \alpha} = \int_{t_1}^{t_2} \left( \frac{\partial I}{\partial x} \eta + \frac{\partial I}{\partial x’} \eta’ \right) \ \mathrm{d} t $$
我们想办法把 $\eta$ 凑出来, 由 $\eta$ 的任意性逼着搞出某个玩意为0. 什么玩意能把 $\eta’$ 变成 $\eta$ 呢? 当然是我们可爱的分部积分. 于是我们把第二项拉出来分部积一下:
$$\int_{t_1}^{t_2} \frac{\partial I}{\partial x'} \eta' = \frac{\partial I}{\partial x'} \eta \big|^{t_2}_{t_1} - \int_{t_1}^{t_2} \left( \frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial I}{\partial x'} \right) \eta \ \mathrm{d}t$$代入回去, 并注意到我们在定义 $\eta$ 时让两端点的 $\eta$ 值为 $0$ 了, 所以把分部出来的第一项略去, 有:
$$\frac{\mathrm{d} S}{\mathrm{d} \alpha} = \int_{t_1}^{t_2} \left( \frac{\partial I}{\partial x} - \frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial I}{\partial x'} \right) \eta \, \mathrm{d}t$$如果此时的函数 $x$ 令 $S$ 有了极值的话, 我们就会有 $\mathrm{d}S/\mathrm{d}\alpha = 0$, 即:
$$\int_{t_1}^{t_2} \left( \frac{\partial I}{\partial x} - \frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial I}{\partial x'} \right) \eta \ \mathrm{d}t = 0$$由 $\eta$ 的任意性, 我们就必有:
$$ \frac{\partial I}{\partial x} - \frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial I}{\partial x’} = 0 $$
综上, 当函数 $x$ 使得
$$ S = \int_{t_1}^{t_2} I[x, x’, t]\ \mathrm{d}x $$
有极值时, 此函数必然满足:
$$ \frac{\partial I}{\partial x} - \frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial I}{\partial x’} = 0 $$
此条件称为欧拉-拉格朗日方程.